Unleashing the Depths of Deep Learning: An In-Depth Exploration of Residual Networks (ResNet)
Introduction
The advent of deep learning has revolutionized the field of artificial intelligence, enabling unprecedented advancements in computer vision, natural language processing, and various other domains. Central to these breakthroughs are deep neural networks—layered architectures that learn hierarchical representations of data. However, as researchers endeavored to build increasingly deeper networks to capture more complex patterns, they encountered significant challenges, notably the vanishing gradient and degradation problems. These issues hindered the training of very deep networks, limiting the potential of deep learning.
In 2015, a seminal development addressed these challenges: the Residual Network, or ResNet. Introduced by Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun, ResNet revolutionized deep learning by enabling the training of neural networks with unprecedented depth—over 100 layers—while maintaining performance and stability. This architecture not only won the ImageNet Large Scale Visual Recognition Challenge (ILSVRC) in 2015 but also became a foundational model in deep learning, cited over 100,000 times in subsequent research.
This article delves into the intricacies of ResNet, exploring how residual learning and skip connections overcome the limitations of deep networks. We will examine the architectural innovations, mathematical formulations, and the profound impact ResNet has had on the field of deep learning.
The Challenge of Training Deep Neural Networks
Vanishing Gradient Problem
Training deep neural networks involves adjusting parameters (weights and biases) to minimize a loss function that measures the difference between the network’s predictions and the actual data. This optimization is typically performed using gradient-based methods, such as backpropagation, which compute gradients of the loss function with respect to the network parameters.
In deep networks, however, gradients can become exceedingly small (or vanish) as they are propagated backward through many layers. This phenomenon, known as the vanishing gradient problem, impedes the network’s ability to learn, as minimal gradient signals fail to update the weights effectively in the earlier layers. Consequently, the network struggles to capture complex features and converges slowly, if at all.
Degradation Problem
Another significant challenge is the degradation problem. Contrary to intuition, simply adding more layers to a neural network does not guarantee better performance. Empirical observations showed that beyond a certain depth, adding layers led to higher training error, indicating that the deeper model performed worse than its shallower counterpart. This degradation is not due to overfitting (as the training error increases), but rather to the difficulty in optimizing deeper networks.
The Emergence of ResNet
In response to these challenges, the authors of ResNet proposed a novel approach: residual learning. The core idea is to reformulate the layers of a neural network to learn residual functions with reference to the layer inputs, instead of learning unreferenced functions.
Residual Learning Concept
Mathematically, let the desired underlying mapping be denoted as , where is the input. Traditional networks aim to approximate directly. In residual learning, the network instead approximates the residual function . Therefore, the original function becomes .
This reformulation is based on the intuition that it is easier to optimize the residual mapping than to optimize the original, unreferenced mapping. In many deep learning tasks, the identity mapping (where ) is a reasonable starting point. Learning the deviations from this identity (the residuals) allows the network to fine-tune the outputs, facilitating training and improving performance.
Skip Connections (Identity Mappings)
To implement residual learning, skip connections (also known as identity mappings) are introduced. These connections bypass one or more layers by feeding the input of a layer directly to the output of a subsequent layer. This mechanism ensures that the input signal is retained and propagated through the network, mitigating the vanishing gradient and degradation problems.
By allowing gradients to flow directly through these skip connections during backpropagation, the network preserves the learning capability of earlier layers, even as depth increases. This architectural innovation is the cornerstone of ResNet’s success.
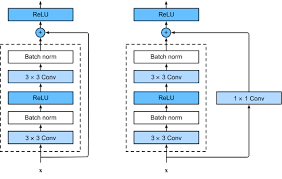
The Residual Block
The fundamental building unit of ResNet is the residual block. It consists of a series of layers and a skip connection that adds the input of the block to its output.
Architectural Details
A typical residual block performs the following operations:
-
First Convolutional Layer:
- Applies a convolution with a filter size of , stride of 1, and padding of 1.
- Ensures that the spatial dimensions of the input and output are the same.
- Followed by batch normalization and an activation function (e.g., ReLU).
-
Second Convolutional Layer:
- Similar to the first, with a convolution, stride of 1, and padding of 1.
- Followed by batch normalization.
-
Skip Connection:
- The input is added element-wise to the output of the second convolutional layer.
- This addition is possible because the dimensions are matched.
-
Activation Function:
- A final activation function is applied to the result of the addition.
This structure can be represented mathematically as: where represents the stacked convolutional layers and is the activation function.
Dimension Matching
For the skip connection to function correctly, the dimensions of and must match. In cases where the dimensions differ (e.g., due to pooling or convolutional layers with strides greater than 1), ResNet addresses the mismatch using:
-
Option A (Zero Padding):
- Pads the input with zeros to match the dimension of .
- Simple and adds no additional parameters.
- However, introduces zero entries that may not contribute useful information.
-
Option B (Projection Shortcut with 1x1 Convolution):
- Uses a convolutional layer with appropriate stride to transform to the desired dimension.
- Introduces additional parameters but allows the network to learn the optimal projection.
Empirical results indicate that Option B often yields better performance due to the learnable parameters that adjust the input mapping.
Benefits of Residual Networks
Training Very Deep Networks
ResNet’s architecture enables the successful training of exceptionally deep networks. The original ResNet demonstrated networks with depths of 50, 101, and even 152 layers, significantly deeper than previous architectures like VGGNet (19 layers). The 152-layer ResNet achieved remarkable performance on ImageNet with a top-5 error rate of 3.57%, surpassing human-level accuracy in some cases.
Overcoming Vanishing Gradients
By allowing gradients to flow directly through skip connections, ResNet alleviates the vanishing gradient problem. The identity mappings ensure that gradients are effectively backpropagated, even through hundreds of layers. This facilitates more effective training of deep networks and captures richer feature representations.
Improved Performance
Residual learning improves not only the convergence of deep networks but also their generalization. ResNet architectures have consistently outperformed their plain (non-residual) counterparts, achieving lower error rates on benchmarks like ImageNet, CIFAR-10, and MS COCO.
Flexibility and Generalization
The residual block is a modular component that can be stacked to create networks of arbitrary depth. Moreover, the concept of residual learning is not limited to image recognition; it has been successfully applied to tasks like object detection, semantic segmentation, and super-resolution.
Applications of ResNet
Image Classification
ResNet has been widely adopted for image classification tasks due to its superior performance and ability to train deep architectures. It won the ILSVRC 2015 classification task and has since become a backbone model for numerous computer vision applications.
Super-Resolution Tasks
In super-resolution, the goal is to reconstruct a high-resolution image from a low-resolution input. ResNet’s ability to retain input signals through skip connections makes it well-suited for this task. By modeling only the residuals (the differences between low and high-resolution images), ResNet efficiently learns the fine details needed for high-quality reconstruction.
Object Detection and Localization
ResNet’s deep feature representations enhance object detection models. Frameworks like Faster R-CNN have integrated ResNet as a feature extractor, improving detection accuracy and localization precision in datasets like MS COCO.
Modeling Dynamical Systems and Differential Equations
An intriguing application of ResNet lies in modeling dynamical systems and solving differential equations. The residual connections resemble numerical integration methods, such as Euler integration, where the next state of a system is computed based on its current state plus a small change. This analogy has inspired the development of continuous-depth models like Neural Ordinary Differential Equations (Neural ODEs), which extend the concept of residual learning to continuous-time systems.
ResNet and Numerical Integration
Connection to Euler Integration
In numerical analysis, the Euler method approximates solutions to differential equations by iteratively adding the product of the derivative and a small time step to the current state:
Similarly, in ResNet, the output of a residual block can be viewed as the current state plus a residual:
This resemblance has sparked interest in interpreting deep residual networks as discrete approximations of continuous dynamical systems. Analyzing ResNet through this lens provides insights into its stability and generalization properties and opens avenues for integrating advanced numerical methods into network design.
Extension to Neural Ordinary Differential Equations
Building on this connection, Neural ODEs represent the transformation of input data as a continuous dynamical system defined by an ordinary differential equation:
By treating depth as a continuous variable, Neural ODEs allow the use of adaptive and higher-order integration techniques, potentially improving efficiency and performance. This approach generalizes the residual learning framework, demonstrating ResNet’s foundational role in advancing deep learning methodologies.
Architectural Variations and Enhancements
Bottleneck Architectures
To improve computational efficiency while maintaining depth, ResNet introduced the bottleneck design for deeper networks. A bottleneck residual block includes three layers:
- 1x1 Convolution (reduces dimensionality)
- 3x3 Convolution
- 1x1 Convolution (restores dimensionality)
This design reduces the number of parameters and computational cost while preserving the network’s ability to learn complex representations.
Wide ResNets and Other Variations
Subsequent research explored modifications to the original ResNet, such as:
- Wide ResNets: Increasing the width (number of channels) of residual blocks instead of depth to improve performance.
- ResNeXt: Incorporating grouped convolutions within residual blocks for better efficiency.
- DenseNet: Connecting each layer to every other layer in a feedforward fashion, inspired by the success of residual connections.
These variations continue to advance the field, building upon the principles established by ResNet.
Impact and Influence
Citation and Adoption
ResNet has had a profound impact on deep learning research and applications. With over 100,000 citations, it is one of the most influential papers in the field. Researchers across domains have adopted its principles, and it has become a standard benchmark architecture.
Influence on Subsequent Architectures
ResNet’s success inspired the development of other models that leverage skip connections and residual learning, such as:
- UNet: Utilized in biomedical image segmentation, incorporating skip connections to combine features from different levels of the network.
- Transformer Models: In natural language processing, architectures like BERT and GPT employ residual connections to facilitate training of deep layers.
Paving the Way for Deeper Networks
By addressing the challenges of training deep networks, ResNet opened the door to exploring even more profound architectures. It demonstrated that depth, when properly managed, can lead to more expressive and powerful models, fueling advances in artificial intelligence.
Conclusion
The introduction of Residual Networks marked a turning point in deep learning, overcoming fundamental obstacles to training deep neural networks. Through the innovative use of residual learning and skip connections, ResNet enabled the effective training of very deep architectures, leading to state-of-the-art performance in image recognition and beyond.
By ensuring that input signals are retained and gradients are effectively backpropagated, ResNet mitigated the vanishing gradient and degradation problems that plagued earlier deep networks. Its architectural principles have not only stood the test of time but have also inspired a plethora of subsequent models and research directions.
As we continue to push the boundaries of artificial intelligence, the lessons from ResNet remain invaluable. It exemplifies how thoughtful architectural design can unlock new capabilities, paving the way for deeper, more powerful networks that bring us closer to human-level performance across a range of complex tasks.
References
- He, K., Zhang, X., Ren, S., & Sun, J. (2016). Deep Residual Learning for Image Recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (pp. 770–778).
- Goodfellow, I., Bengio, Y., & Courville, A. (2016). Deep Learning. MIT Press.
- Chen, T. Q., Rubanova, Y., Bettencourt, J., & Duvenaud, D. (2018). Neural Ordinary Differential Equations. In Advances in Neural Information Processing Systems (pp. 6571–6583).